Foreword

I've decided that I need to stretch my security brain again, and after watching a number of LiveOverflow's post-CTF write-up videos, I thought I'd start with some practice CTFs.

For the uninitiated, CTF stands for Capture the Flag. They're essentially competitions which invite people to think creatively and solve security challenges in order to "steal the flag". Typically these can be "Attack/Defence" challenges, where you have to protect your own flag while trying to steal the other team's, or they can be Jeopardy-style where you steal from the organiser with pre-set problems to solve. CTFs tend to be attached to big events with a limited lifespan, such as DEF CON or BSides.

I've found myself most comfortable with Jeopardy-style CTFs, mostly because I'm not in it to win it, I'd much rather pick and choose what I'm going to work on and be happy when I solve it.

I recently came across 247CTF, a moderately new site which hosts a number of different flag challenges across different categories with their difference being, their challenges are always live. This is where I'll start out.

Challenge Info permalink

+----------------+--------------------------------------------+
| CTF Name       | 247CTF                                     |
| Challenge Name | An Exclusive Key                           |
| Description    | Decrypt the provided file to find the flag |
| Category       | Cryptography                               |
| Points         | 200                                        |
+----------------+--------------------------------------------+

In this challenge, we're given an encrypted file and we're asked to find the encryption password and decrypt the file.

Method permalink

First things first, let's see what info we can glean or assumptions (we'll be seeing a lot of those) we can make before actually getting into solving the problem.

We're told that the file was encrypted with XOR which narrows down the problem a lot and lets us consider some reusable techniques from other CTF/cryptoanalysis problems - such as block size detection using normalised Hamming distance. Let's try that out first.

Step 1 - Work out the normalised Hamming distance of a range of block sizes permalink

In order to work out the block size of the XOR key, we need to:

1. Split the cipherblock into n-length blocks, where n is in the range of 1 to some higher number. Let's pick 256.
2. Work out the Hamming distance of the first couple of n-length blocks, and take the average.
3. Normalise the value by dividing it by the length of the block, that way values will be relative to each other, and it'll be easier to work through later.
4. Take the lowest 4-5 resulting distances. One of these is likely to be your key length.

Calculating the Hamming distance of values is surprisingly easy given we're working with binary. Just XOR the two values, and then count the number of 1s in the result.

An illustrated example would look like:

(15)       (109)       (98) 
00001111 ⊕ 01101101 =  01100010 -> Hamming Distance = 3

Looks easy enough. So it's time to code that up. We'll be doing this in Python, and the full code is available on Gitlab.

The first difficult we encounter is Python's handling of binary data, and managing representations of it. It's doable, but requires long chains of parsing of different datatypes, so the code can sometimes look a little... heavy. This is only a problem as far as the Hamming distance and Xor code goes.

def xor(a, b):
  x = [i ^ j for i, j in zip(a, b)]
  return bytes(x)

def hamming_distance(a, b):
  """
  The easiest way to work out the number of 1s in a byte in 
  Python is to convert it to a hex string, parse that as a number,
  convert that to Binary and then count the number of "1s".
  """
  return bin(int(xor(a, b).hex(), 16).count('1')

The next step is to read out file, and break it up into n-length blocks. We can achieve this by taking slices of the file at n-stop increments, and creating a new list of these blocks.

While we're at it, we can also write our scoring function, which just uses what we've written already to build a dict of possible block sizes and their associated normalised Hamming distance.

from statistics import mean

fo = open("exclusive_key", 'rb')
f = fo.read()

def bin_split(b, size):
  return [b[i: i + size] for i in range(0, len(b), size)]

def scoring(f):
  scores = {}
  for i in range(1, 256):
    split = bin_split(f, i)
    h = [] 
    for j in range(1, 6):
      h.append(hamming_distance(b[0], b[j]))
    havg = mean(h) # Averaging the results
    score = havg/i # Normalising the result
    scores.update({i: score})
    

The results from this actually ended up being quite interesting. You might already be able to see why, but let's dig into it.

+------+------------+--------------------+
| Rank | Block size | Hamming distance   |
| #1   | 160        | 2.9537500000000003 |
| #2   | 200        | 2.957              |
| #3   | 240        | 2.9616666666666664 |
| #4   | 40         | 2.965              |
| #5   | 1          | 3.4                |
+------+------------+--------------------+

As predicted, we see that there are a few results that only minutely differ which means we were right to pick a larger range of results to work through. We can also rule out a single-byte XOR key as it's unlikely that this would end up being a 200 point challenge.

But perhaps most interestingly, ranked at #4 is a block size of 40. This catches my attention as it just so happens to be the same length as the flag used by 247CTF. Knowing this, let's indulge the possibility that the flag isn't in the file, but that instead the flag is the key encrypting the file. That's fine, XOR is a bi-directional operation so that would make sense anyways. In that instance, we at least know where we're looking for the key.

As I just mentioned, XOR is reversible. If you have a ⊕ b = c, then c ⊕ a = b, and vice-versa. If we roll with the assumption (there's that word again) that the key is the flag, then we know 7 consecutive characters of the key already, 247CTF{. What happens if we try and XOR that key against the file.

Let's write some more code to figure that one out.

# itertools.cycle will help us apply the key in 40-byte blocks
from itertools import cycle 

def decrypt(cb, k):
  return xor(cb, cycle(key))

# We need to encode the key to Bytes to make sure xor works
key = "247CTF{".encode("utf-8")
test_1 = decrypt(f, key)

with open("test.bin", "wb") as wb:
  wb.write(test_1)

Obviously, if we don't have the full key, then we're only going to get decoded information for the first couple of bytes, everything else will just be garbage data (I'm talking in certainties because of that A word again). What does xxd tell us.

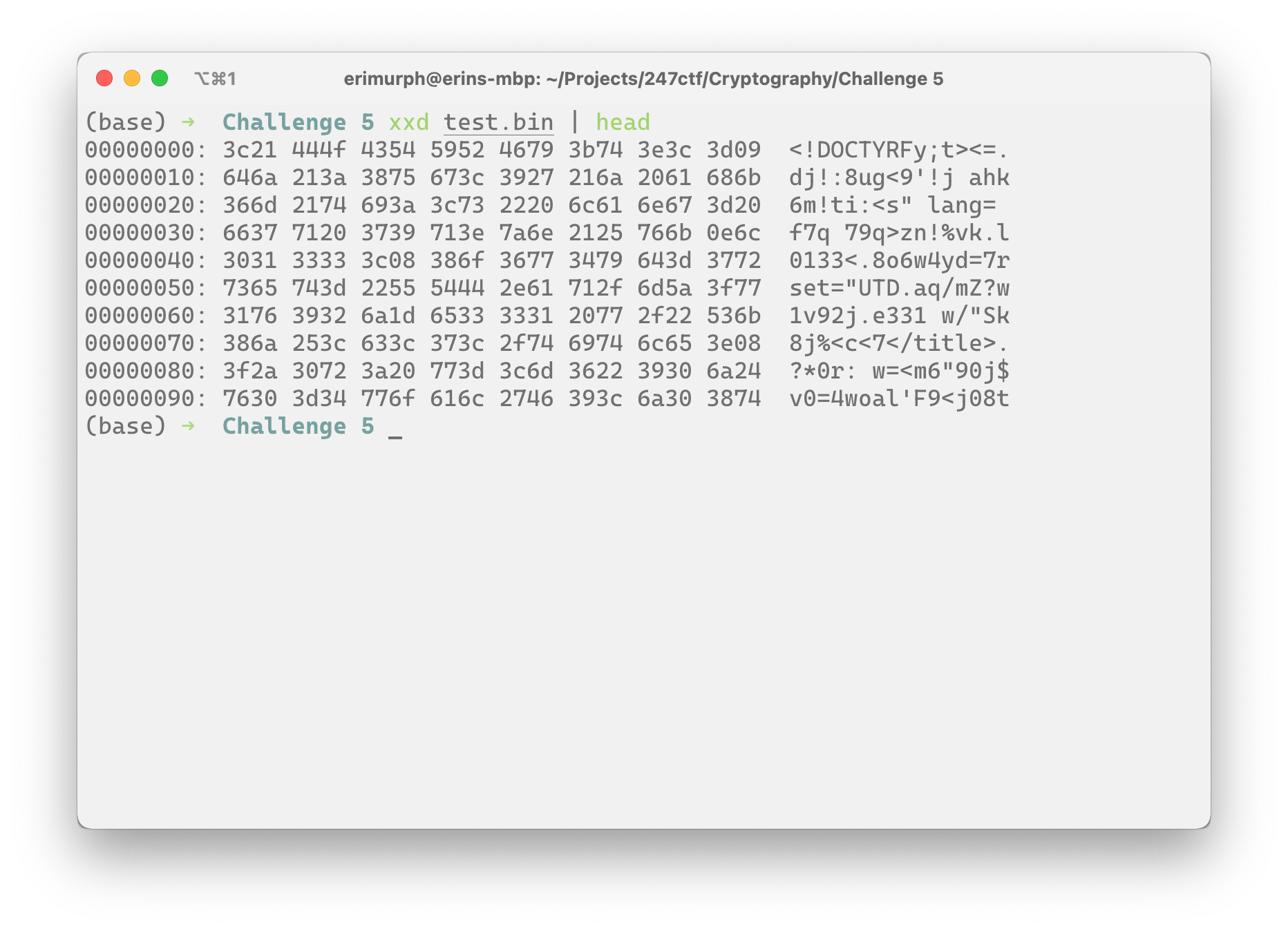
Bingo. We've got HTML! Our encrypted file is a web page (probably). So our first couple of assumptions were right. Was it just luck? Are we on a roll? I don't know, and I don't particularly care. So let's make some more.

Assumptions

1. The file is definitely HTML. Due to the presence of <!DOCTY at the very beginning of the file.
2. We can finish off that first line with <!DOCTYPE html>.
3. Immediately after a newline, there will be a <html> tag.

We're not quite in the clear yet though. We've only found the first 15 bytes of a 40 byte flag, and assumption #3 while helpful, will hinder us. You see, <html> isn't just a one-and-done. There are different attributes that, while standard, are sometimes used and sometimes not, and the order isn't necessarily the same from site to site. Let's list out some different options for our flag decryption key.

<!--Option 1 (22)-->
<!DOCTYPE html>
<html>

<!--Option 2 (32)-->
<!DOCTYPE html>
<html lang="en">

<!--Option 3 (59)-->
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">

<!--Option 4 (70)-->
<!DOCTYPE html>
<html lang="en" xmlns="http://www.w3.org/1999/xhtml" >

<!--Option 5 (83)-->
<!DOCTYPE html>
<html lang="en" xmlns="http://www.w3.org/1999/xhtml" xml:lang="en">

As you might be able to already see, this could be a problem. I've noted down the number of bytes each option presents as well, including newline characters. We have three options above the 40 character limit, which means we can easily rule out all of the options if they don't match beyond <html. Let's test that theory.

test2a = "<!DOCTYPE html>\n<html>\n".encode("utf-8")
test2b = "<!DOCTYPE html>\n<html lang=\"en\">".encode("utf-8")
test2c = """<!DOCTYPE html>\n<html lang=\"en\"""
            xmlns=\"http://www.w3.org/1999/xhtml\">".encode("utf-8")
test2d = """<!DOCTYPE html>\n<html lang=\"en\"""
            xmlns=\"http://www.w3.org/1999/xhtml\" 
            xml:lang=\"en\">""".encode("utf-8")

result2 = [decrypt(f, test2a), decrypt(f, test2b),
               decrypt(f, test2c), decrypt(f, test2d)]
    result2n = 1
    for i in result2:
        with open(f"result2_{result2n}.txt", "wb") as w:
            w.write(i)
            result2n += 1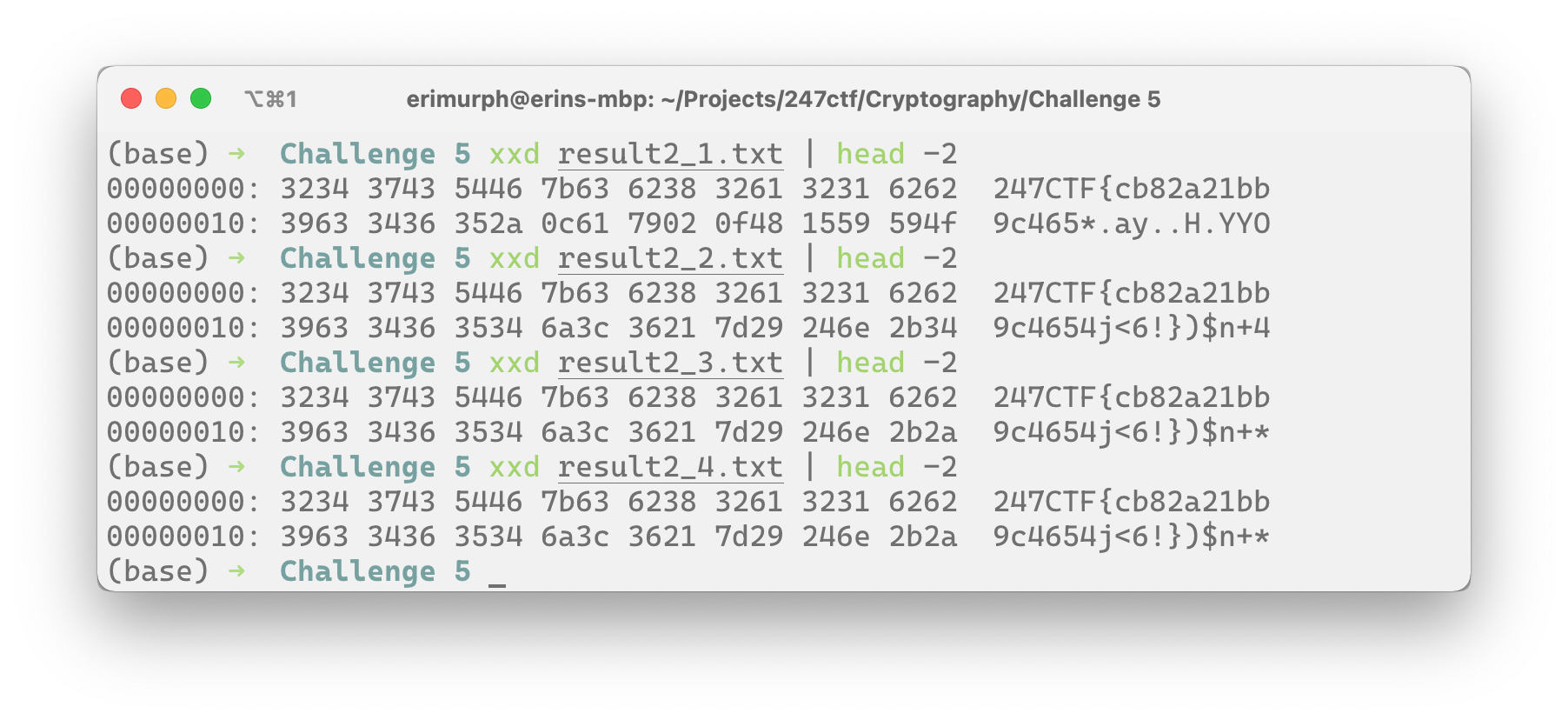

Something we know for sure is the format of the flag. It's a 40-character string, always starting with 247CTF{, ending in }, with a 32 character hex string between the braces. And well... there are non-hex characters where the hex characters should be. Hmm. We at least know we're on the right track with the html format, if we go back to our first attempt, what other information from the file can we use to help us find the flag?

Oh ho ho.... That's really interesting.

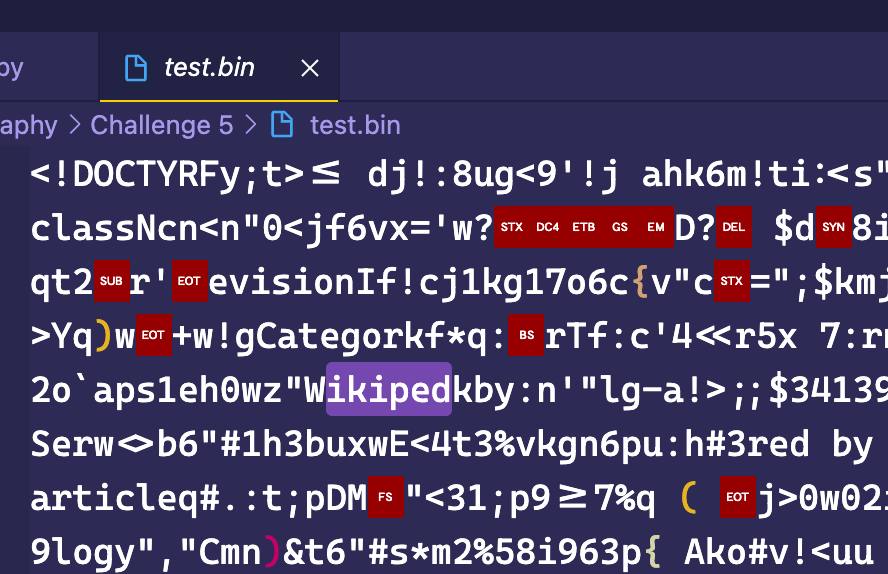
Is that... Wikipedia? Is Jimmy Wales trying to ask for my money through the means of a CTF? Either way, if it is a Wikipedia page that has been saved, then we should check out what Wikipedia page source looks like and maybe that will help us out.

<!--From wikipedia.org-->

<!DOCTYPE html>
<html class="client-nojs" lang="en" dir="ltr">
<head>
<meta charset="UTF-8"/>
<title>Exclusive or - Wikipedia</title>

I've never come across class or dir as attributes for html tags. I wonder what those mean.

By default, Modernizr will rewrite <html class="no-js"> to <html class="js">. This lets hide certain elements that should only be exposed in environments that execute JavaScript.

So it looks like the class attr comes from Modernizr, which is a feature detection library which allows JS websites to be served to non-JS capable clients. Anyways, that's enough rambling about how Jimmy wants to serve his bytes. Let's unlock that file...

Time to plug that into our decryption tool, minus the excess bytes.

solve = "<!DOCTYPE html>\n<html class=\"client-nojs".encode("utf-8")

with open("solve.txt", "wb") as wb:
  wb.write(decrypt(f, cycle(solve))

And the moment of truth...

via GIPHY

We did it! We got the flag. But I'm sure you're as interested as I am as to what wiki article it is? Well, aptly...

Footnotes

I hope to write more of these, so keep your eyes peeled on the blog.